详解冒泡排序，不能再详细了！

发表于

在我们日常开发中，排序是非常常见的一种需求，提供一组数据元素，把这些数据元素按照一定的规则进行排序。比如微信公众号的文章是按照文章的发布时间进行排序，再比如在电商类APP中查询一些商品，按照商品的价格进行排序，更复杂的会根据用户的喜好进行排序。

在平常的项目中，简单的排序需求我们可以使用数据库提供的order by 语句进行排序，我们也可以使用JDK提供的工具方法（比如Arrays.sort()）进行排序，这些排序方式都是别人封装好的，内部肯定使用了某种排序算法。我们有必要去了解一些经典的排序算法，接下来的几篇文章将介绍一些常见的排序算法：冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、计数排序、基数排序、桶排序。其中快速排序甚至被誉为20世纪科学和工程领域的十大算法之一。

本篇文章将介绍冒泡排序，冒泡排序应该是我们最早接触到的一种排序算法了，记得笔者应该是在C语言课上接触到的冒泡排序，那时候不是很理解，只是记住了代码实现。接下来我将一步一步演示冒泡排序的过程。

冒泡排序

冒泡排序（Bubble Sort）是一种简单的排序算法，它通过依次比较相邻的两个元素，判断两个元素是否满足大小关系，如果不满足则交换两个元素，每一次冒泡会让至少一个元素移动到它应该在的位置，这样n次冒泡就完成了n个数据的排序工作。这个算法的排序过程与气泡从水中往上冒的情况很相似，故美其名曰：冒泡排序。

需求：

排序前：4, 6, 3, 5, 2, 1

排序后：1, 2, 3, 4, 5, 6

算法过程：

  • 比较相邻的元素，如果前一个元素比后一个元素大，就交换这两个元素；
  • 对每一对相邻元素做同样的操作，从开始第一对元素到结尾最后一对元素，最终最后位置的元素就是最大值。
  • 除了已排序的，针对剩余所有的元素重复上述两个步骤；
  • 重复前三步，直到排序完成。

每一次冒泡会让至少一个元素移动到它应该在的位置，右边是已排序位置，左边是未排序位置。

可以发现，每经过一次冒泡会让至少一个元素移动到它应该在的位置，比如第3次冒泡之后元素4、5、6已经进入已排序位置，它们没必要参与后续的冒泡了。

最后剩下一个元素1，没有继续冒泡的必要了，6个元素最多经过5次冒泡，就可以完成排序。

为了便于理解冒泡排序的过程，我从网上找了一幅动图给大家：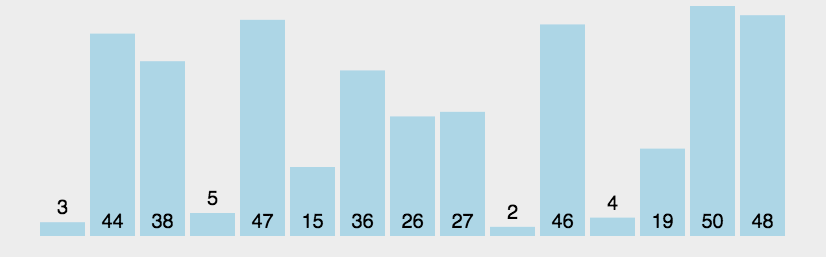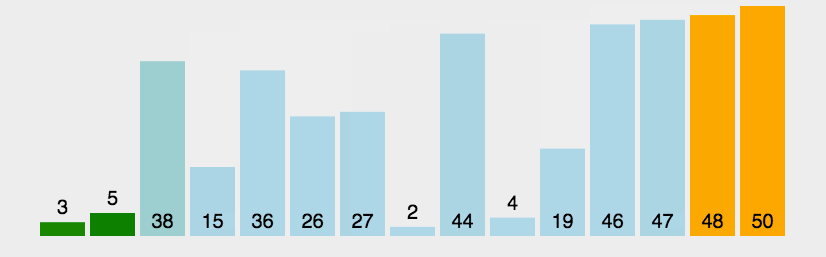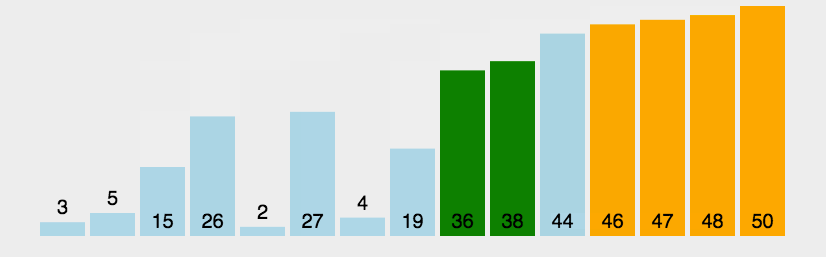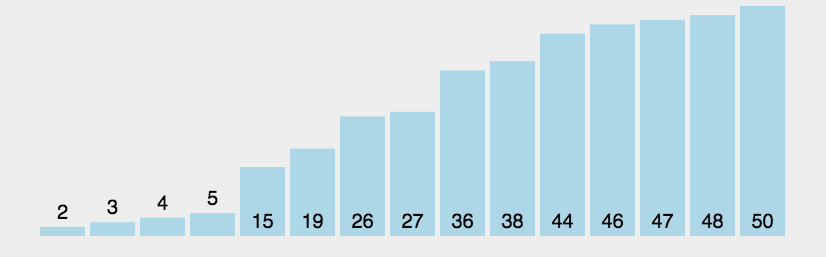

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import java.util.Arrays;

public class BubbleSort {

    public void sort(int[] arr) {
        int len = arr.length;
        for(int i = 0; i < len-1; i++) {
            System.out.print("第" + (i+1) + "次冒泡");

            for(int j = 0; j < len-1 - i; j++) { // 参与冒泡的元素索引
                if(arr[j] > arr[j+1]) {
                    swap(arr, j, j+1);
                }
            }
            System.out.println(Arrays.toString(arr));
        }
        System.out.println("排序后：" + Arrays.toString(arr));
    }

    /**
     * 交换元素
     * @param arr
     * @param i
     * @param j
     */
    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

上述代码存在一个问题，就是当元素已经有序的时候，程序还是会继续冒泡无法提前结束，我们可以通过一个交换的标识位来判断是否需要提前结束，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void sort(int[] arr) {
    int len = arr.length;
    for(int i = 0; i < len-1; i++) {
        System.out.print("第" + (i+1) + "次冒泡");
        // 是否交换的标识位，用于提前结束冒泡
        boolean flag = false;
        for(int j = 0; j < len-1 - i; j++) { // 参与冒泡的元素索引
            if(arr[j] > arr[j+1]) {
                swap(arr, j, j+1);
                flag = true;
            }
        }
        System.out.println(Arrays.toString(arr));

        if(!flag) {
            break;
        }
    }
    System.out.println("排序后：" + Arrays.toString(arr));
}
总结

1、冒泡排序的时间复杂度是多少？

最好情况下，要排序的数据已经是有序的了，我们只需要进行1次冒泡操作，所以最好情况的时间复杂度是O(n)，而最坏的情况是，要排序的数据刚好是相反的，我们需要进行n-1次冒泡操作，所以最坏情况的时间复杂度为O(n^2)。

2、冒泡排序的空间复杂度是多少？

冒泡排序过程只涉及相邻数据的交换操作，只需要常量级的临时空间，所以它的空间复杂度为O(1)。

3、冒泡排序是稳定的排序算法吗？

冒泡排序过程，只有交换才可以改变两个元素的前后顺序，为了保证冒泡排序算法的稳定性，当相邻的两个元素大小相等的时候，我们不去做交换，相等的两个元素排序前后顺序保持不变，所以冒泡排序是稳定的排序算法。

坚持原创技术分享，您的支持将鼓励我继续创作！